SAP2000: Modello ad elementi finiti di una connessione trave colonna

Argomento: Guida alla modellazione di un collegamento in acciaio: T-Stub, buckling, nonlinear buckling.
Autore: Leonardo Bandini
Contatto: supporto@csi-italia.eu

I modelli di calcolo sviluppati sono scaricabili in fondo alla presente guida

Introduzione

Il presente documento ha lo scopo di mostrare le operazioni da seguire per la modellazione di un collegamento trave colonna in campo non lineare. In particolare si illustreranno le procedure per la modellazione geometrica, riproduzione del contatto tra flangia di testa e piattabanda, bulloni, definizione della plasticità combinata mediante Von Mises, inserimento delle imperfezioni geometriche a seguito di una analisi di buckling, perfezionamento delle condizioni al contorno e definizione dell’analisi in controllo di spostamento, atta alla determinazione della curva di capacità, momento-deformazione del collegamento. Tale modellazione ha lo scopo di mostrare le procedure che possono essere facilmente adattate a casi reali. 

Questa la storia delle deformazioni step-by-step, con evidenziato il comportamento d’instabilità locale per imbozzamento del pannello d’anima del collegamento. Si eseguiranno due versioni dello stesso modello: con e senza irrigidimenti del pannello d’anima della colonna.

(fare click sulle immagini per vederne l’animazione dei successivi step)

     

 

   

Step #1, geometria

Data la semplice geometria di questo nodo si è operato direttamente in SAP2000, è possibile importare geometrie più complesse utilizzando diverse procedure di interscambio: IFC, DWG, DXF… 

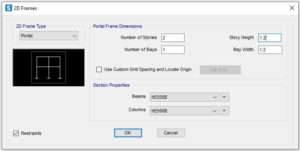
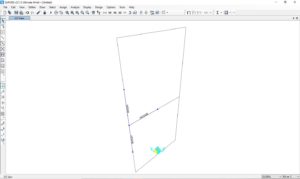
Si parte dall’utilizzo del template di un frame 2D:

Si procede a lasciare la porzione del modello di interesse, ovvero, una porzione di circa 60 cm di elementi frame intorno al nodo a tre vie tra colonna (HEB500) e trave (HEB500).

 

Si seleziona il nodo d’intersezione e si effettua una disconnessione degli elementi sul nodo (menu Edit-Edit Points-Disconnect), in questo modo, nell’intersezione ci saranno 3 nodi, uno per ogni elemento finito incidente. Si seleziona il nodo del frame della trave e lo si sposta del semi spessore della colonna sommato allo spessore dell’end-plate della trave, poi successivamente, operando sul nodo delle due colonne, si effettua una connessione. Il risultato sarà il seguente:

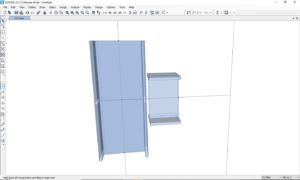
A questo punto si selezionano i tre frame e dal menu Edit, si sceglie il comando di estrusione: Edit-Extrude-Convert Lines to Areas. Adesso ci saranno elementi area per ogni piattabanda ed anima di elemento. 

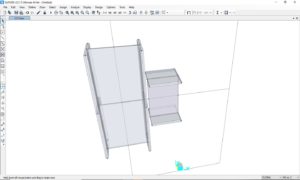
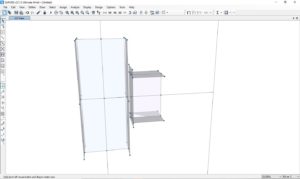
Si modella la flangia di testa, è possibile aiutarsi con operazioni di estrusioni da frame di supporto. Il risultato è il seguente:

La geometria di partenza è conclusa, si procederà successivamente alla meshatura, ma prima la definizione dei materiali ed altri elementi utilizzati.

Step #2, definizioni di materiali ed elementi

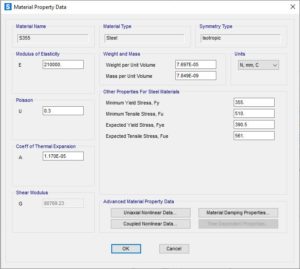
Definizione del materiale acciaio utilizzato: S355 da libreria dei materiali.

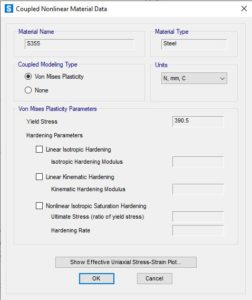
Si proceda a visualizzare la legge costitutiva tensione-deformazione non lineare ed anche i dati dell’accoppiamento delle tensioni, utilizzando il metodo di Von Mises. 

Nel caso specifico si sono utilizzate le leggi proposte, quindi si procede alla sola visualizzazione, tuttavia è possibile adottare leggi di tipo EPP (Elastico Perfettamente Plastico), di tipo incrudenti definite in forma completamente parametrica. 

La stessa cosa vale per la teoria di plasticizzazione scelta. Nel caso specifico si è scelto Von Mises, ma è possibile modificarne parametricamente l’incrudimento.

Questo sarà quindi il modello di comportamento del materiale ottenuto:

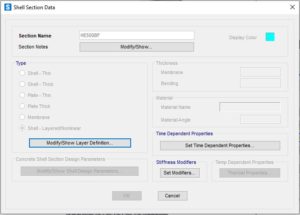
Definizione degli elementi shell utilizzati: Nonlinear Layered Shells.

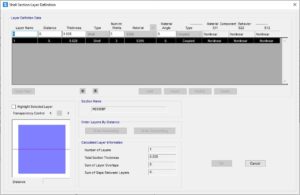
Qui fare attenzione alle definizioni: sarà presente un unico layer, dello spessore dell’elemento considerato (piattabanda, anima, flangia di testa, eventuali nervature di rinforzo), questo layer avrà 3 punti di calcolo nello spessore, questo servirà per coglierne il meccanismo per deformazioni fuori piano (comportamento a piastra). Il layer sarà di tipo “Coupled“, ereditando così l’accoppiamento delle tensioni secondo il metodo VM descritto nel materiale. 

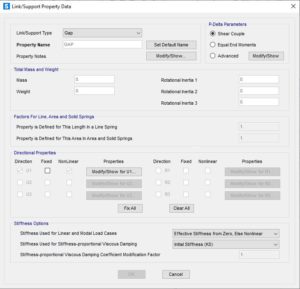
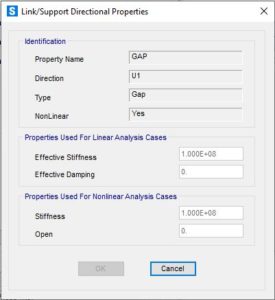
Adesso la definizione per il contatto a compressione tra flangia di testa e piattabanda: elemento di tipo GAP. Tale elemento, come noto, è una molla con una rigidezza definita che lavorerà solo in compressione. Consentirà di cogliere, a seguito delle deformazioni degli elementi, meccanismi T-Stub. Il link sarà attivo solo sul suo grado di libertà U1, ovvero quello longitudinale dell’elemento stesso, si lascerà la connessione a taglio ad opera dei link utilizzati per i bulloni.

Le unità di misura sono kN,m, una rigidezza di 1E8kN/m è da considerarsi infinitamente rigida a compressione, come richiesto in un semplice modello di contatto, saranno gli elementi adiacenti a sviluppare la deformazione. 

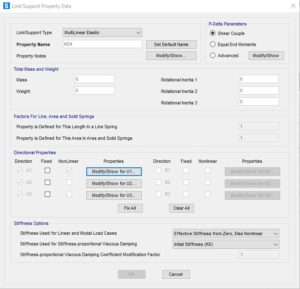
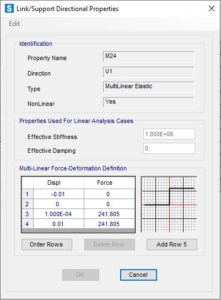
I bulloni sono invece modellati tramite un semplice link di tipo Multilinear Elastic, lo scopo dell’analisi sarà quello di riprodurre un comportamento statico, atto alla determinazione della curva di capacità del nodo, nel caso in cui servisse riprodurre il comportamento ciclico, con inversione di cicli di carico e scarico, si suggerisce l’adozione di un link Multiliner Plastic con Incrudimento Cinematico. 

 

La direzione U1, rappresenterà il comportamento a trazione del bullone, la compressione è mantenuta a zero. Si è volutamente scelta una legge di tipo EPP per la trazione, ma è possibile anche in questo caso passare incrudimento e prevedere strength loss a seguito del raggiungimento della deformazione limite. Per il taglio si è scelto di mantenere il comportamento rigido, ma è possibile simularne leggi plastiche o attritive. 

Step #3, meshatura e tracciamento dei link

Si è proceduto ad una meshatura uniforme di tutto il modello e si sono inseriti i link. Tale inserimento è stato effettuato con una semplice operazione di array. 

Questo il risultato:

Step #4, vincoli e condizioni al contorno

Come anticipato, lo scopo di tale analisi è determinare la curva di capacità del nodo, derivante dalla plasticizzazione e dalla instabilità locale delle membrature. Si sceglierà di procedere ad un’analisi in controllo di forza. Questo ha guidato alla definizione delle condizioni al contorno, in particolare si è inserito un sistema di forze auto-equilibrato, costituito principalmente da un taglio ed un momento applicato sulla trave, con le relative forze di equilibrio applicate sulla porzione superiore della colonna, mentre la base della colonna è stata vincolata mediante l’applicazione di restrainer U1,U2 ed U3, in tutti i nodi in basso. 

Il nodo viene quindi analizzato soggetto ad un sistema di forze costanti (che rappresentano la parte statica), in particolare uno sforzo assiale derivante dalla colonna superiore, ma potrebbero essere applicati i carichi anche per le altre caratteristiche di sollecitazione, ed un sistema di forze variabili (step-by-step) che rappresentano i carichi variabili eccezionali: sisma, vento, esplosione…

All’estremità superiore della colonna e della trave, possono essere disposti dei body constraint, per facilitare l’inserimento di sollecitazioni puntuali, queste sollecitazioni potrebbero essere lette dal modello completo unifilare della struttura, consentendo così di passare le reali condizioni al contorno derivanti da un modello completo.

Step #5, analisi per le condizioni iniziali

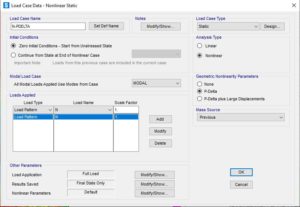
I carichi mantenuti costanti, verranno applicati come condizione iniziale: un precarico di tutte le membrature. Questa analisi sarà un’analisi statica non lineare (comprensiva di effetti P-Delta) eseguita in controllo di forza. 

Alla fine di questa analisi, le membrature avranno lo stato di sollecitazione (e rigidezza) dipendenti dalla condizione di precarico. A questo punto si eseguirà un’analisi di buckling, atta a determinare la forma d’instabilità che si utilizzerà come imperfezioni locali. Il metodo è descritto in AISC come metodo Diretto: Direct Analysis. Per la descrizione completa del modello si rimanda alla visione dei numerosi webinar dedicati all’argomento degli effetti del secondo ordine presenti in:  https://www.csi-italia.eu/video-seminari/

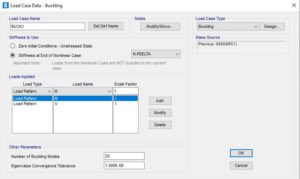
Si definisce quindi l’analisi di buckling che servirà per la determinazione delle imperfezioni iniziali:

Si esegua adesso le due analisi appena definite. 

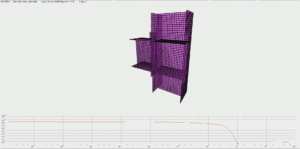
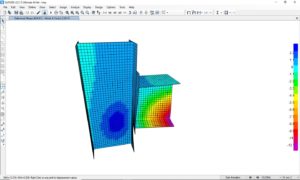
Questa la deformata del primo modo d’instabilità, si noti l’instabilità per imbozzamento del pannello d’anima. Si utilizzerà questa forma per innescare le imperfezioni, seguendo la semplice procedura di seguito riportata. 

Deformata del primo modo d’instabilità:

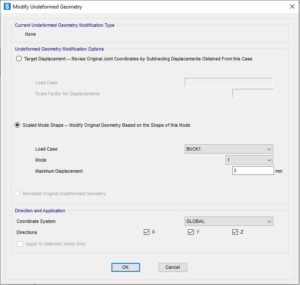
Dal menu di analisi si scelga l’opzione di modifica della forma geometrica del modello: Analyze-Modify Undeformed Geometry.

Per l’entità della deformazione si suggerisce un valore di circa 1/250 della dimensione delle membrature. Tale valore è arbitrario, si fa notare che serve come innesco agli effetti del secondo ordine, un eventuale sottostima delle imperfezioni o sovrastima, produrrebbe una modifica della sola componente al primo ordine degli effetti dell’imperfezioni, ma il secondo ordine risulterebbe circa il medesimo. Si sconsiglia di non inserire tale imperfezione, è necessaria per l’innesco del meccanismo d’instabilità. in modelli elastici, di norma, oltre ad inserire le imperfezioni geometriche, come descritto in AISC, si deve considerare anche la perdita di rigidezza indotta dalle plasticizzazioni. In questo modello non serve altro, dal momento che l’analisi sarà condotta in regime plastico, quindi gli elementi finiti perderanno (o in generale varieranno) rigidezza sia per forma (grande spostamento), che per carichi (P-Delta), che per stato tensionale (plasticità secondo VM).

Il modello si presenterà così: seppur in modo quasi impercettibile, gli elementi finiti sono automaticamente disposti tenendo in conto della distorsione indotta dalla forma scelta:

(Si faccia click sull’immagine per ingrandirla e vedere le deformazioni indotte dalle imperfezioni geometriche iniziali).

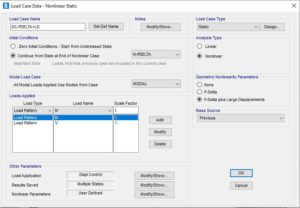
Step #6, analisi statica non lineare

Questo è l’ultimo step della procedura di modellazione: la definizione dell’analisi che servirà per il tracciamento della curva di capacità del nodo. L’analisi è di tipo statico non lineare, include gli effetti P-Delta e Grandi Spostamenti, essa partirà dalla fine dell’analisi precedente, ereditandone deformazioni, carichi e rigidezza e sarà condotta a controllo di spostamento.

 

Si è scelto di monitorare lo spostamento Uz del nodo centrale più esterno della piattabanda superiore della trave. 

Risultati

La curva di capacità monitorata è ottenuta in termini di Momento-Deformazione. Come deformazione si è scelto il nodo coincidente al punto di controllo, ma si può ovviamente guardare in termini di Momento-Rotazione. Allo scopo si è definita una SectionCut per il tracciamento del momento sulla trave, in corrispondenza della flangia. Nel caso in cui si voglia ricavare la rotazione, si può definire un Generalized Displacement. 

Si può notare come la duttilità d’insieme sia limitata dall’instabilità locale del pannello d’anima, come del resto sia dipendente dallo stato di compressione della colonna, indotto dai carichi statici. 

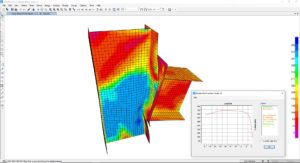
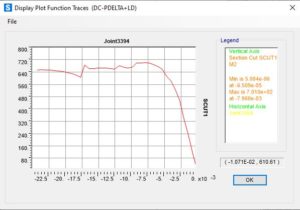
Curva di capacità condotta con il minimo sforzo assiale della colonna

Si fa notare il collasso avvenuto per schiacciamento ed imbozzamento del pannello d’anima. 

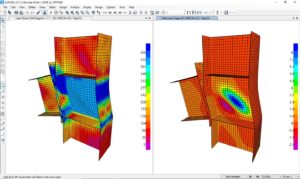
Animazione della progressione delle tensioni di VM sugli elementi (fare click sull’immagine per attivarla):

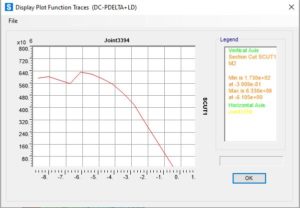
Curva di capacità dello stesso nodo nella condizione di più elevata compressione, dove si può vedere come sia la resistenza che la duttilità, siano diminuite a seguito di un’instabilità anticipata, rispetto al caso precedente. 

Ulteriori sviluppi

Si è estesa la modellazione ad altri casistiche di nodo, per esempio la presenza di nervature d’irrigidimento del pannello nodale: “continued plate”.

Fare click sull’immagine soprastante per vederne l’evoluzione step-by-step.

 

Come si è esteso lo studio agli effetti ciclici, analizzando in forza con cicli di carico e scarico di forma armonica, le descrizioni ed i risultati verranno pubblicati in altri articoli.

Link ai modelli di calcolo qui presentati: scarica modelli.