Il carrello è attualmente vuoto.
- Introduzione
- Analisi pushover - parte I
- Analisi pushover - parte II
- Analisi pushover - parte III
- Analisi pushover - parte IV
- Esempio applicativo
- Video seminario
- Modelli di calcolo e dispense
Analisi Pushover: parte III
Cerniere plastiche, definizioni per: travi, pilastri e setti
In letteratura e di conseguenza in SAP2000 o ETABS esistono diversi modi di formulare la legge costitutiva delle cerniere plastiche. In prima battuta, si determina la posizione dei possibili meccanismi plastici o rotture fragili a seguito di forze orizzontali e deformazioni corrispondenti. Tali posizioni possibili, schematicamente riportate in Figura 9, saranno oggetto di un “controllo” durante ogni passo dell’analisi ed introdurranno una modifica alla rigidezza dell’elemento finito che le contiene. Ci sono diverse formulazioni di cerniere plastiche, comunemente note come Plastic Hinge o più semplicemente Hinge. Procediamo con una prima classificazione di esse:
- sulla base del tipo di formulazione:
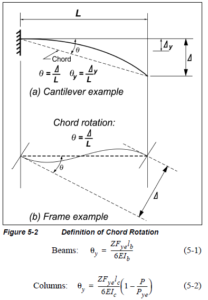
- cerniere di tipo rotazione alla corda;
- cerniere plastiche con modelli a fibre.
- sulla base del tipo di controllo:
- cerniere plastiche a controllo di deformazione (duttili);
- cerniere plastiche a controllo di forza (fragili);
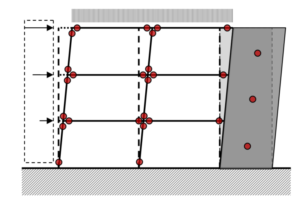
Figura 9: possibili formazioni di cerniera plastica
Le possibili posizioni corrispondono normalmente alle estremità di ogni elemento strutturale, ipotizzando un comportamento shear type per il telaio, si può immaginare che siano l’inizio e la fine di ogni trave e colonna. Anche per i setti si può ragionare in modo simile, ipotizzando la formazione di cerniera plastica alla base degli stessi, deformazione di pura mensola, oppure, con l’ipotesi di eventuale interazione strutturale, estendere tale controllo a tutta la parete.
Cerniere plastiche del tipo rotazione alla corda
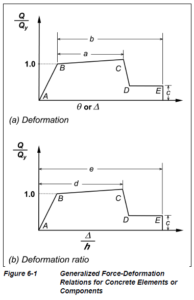
In tale cerniera plastica, la legge costitutiva è fissata misurando, come deformazione la rotazione della membratura in riferimento alla corda. Si immagini, per esempio, una trave di un telaio, la corda è rappresentata dall’indeformata della trave stessa. Si applichi ad essa una deformazione via, via crescente. Sotto questa ipotesi, la legge Momento-Rotazione, può essere linearizzata a tratti come in Figura 10. Le similitudini qualitative con la curva di capacità complessiva della struttura, riportata in Figura 1, sono ovviamente molte. Per piccole deformazioni, la cerniera rimane elastica, tratto tra A e B. Si arriva alla rotazione che corrisponde al momento di snervamento, punto B. Superata questa deformazione, la rigidezza della cerniera decade, mantenendo un certo incrudimento. Tratto tra B e C. In C si raggiunge la rotazione limite, il valore ultimo di questa rotazione per la quale la membratura si può immaginare danneggiata ma ancora resistente. Superata questa rotazione, si ha una rottura locale. La sezione porta ancora del carico, ma si entra nella fase definita perdita di resistenza, tratto tra C e D. La resistenza è rimasta a valori bassi, definiti residuo di resistenza, valore c del grafico. Continuando ancora a ruotare la cerniera, si raggiunge il valore contrassegnato con la lettera E, vero collasso.
Figura 10: cerniera plastica del tipo rotazione alla corda
I dati a, b e c si chiamano normalmente parametri di modello della cerniera plastica, essi rappresentano il vero dato di input della cerniera plastica: ne fissano la legge comportamentale (backbone curve). Ci sono diversi metodi per ottenere tali dati comportamentali di una cerniera plastica di questo tipo. Per una trave tali dati dipendono da tre discriminanti: rapporti di armatura (lembo superiore ed inferiore della trave), passo delle staffe, sovra resistenza della trave a taglio, nei confronti della rottura del puntone compresso. Per un pilastro, il ragionamento è analogo, ma il primo discriminante è la presenza e l’entità di sforzo assiale. Lo stato di compressione riduce la duttilità di una sezione in c.a. La legge comportamentale di una cerniera del tipo rotazione alla corda, può essere tracciata in automatico da SAP2000 e da ETABS (si veda Figura 12, Figura 13, Figura 14).
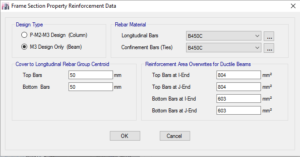
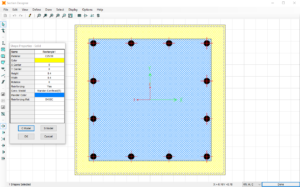
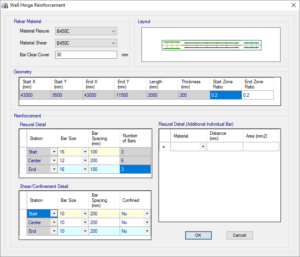
Figura 11: assegnazione delle armature nelle travi per il calcolo della duttilità della sezione
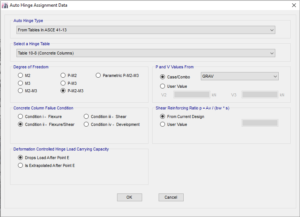
Figura 12: inserimento di una cerniera di tipo automatico secondo FEMA o ASCE41
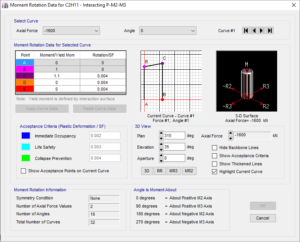
Figura 13: caratterizzazione dei parametri della cerniera plastica
Figura 14: determinazione automatica della legge comportamentale e dei criteri di accettazione della cerniera plastica
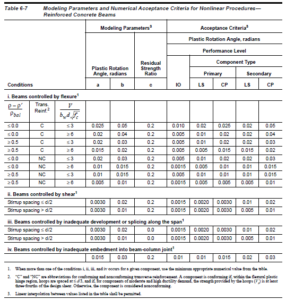
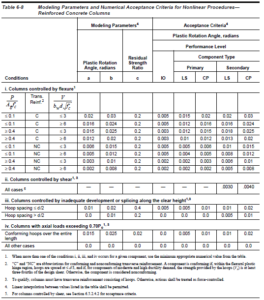
Oltre ai parametri comportamentali, si definiscono i limiti rotazionali di accettazione. Ad ogni stato limite: danno limitato, danno severo e collasso si associano delle rotazioni limite, superate le quali vengono superati i relativi stati limite. Tali valori dipendono dagli stessi discriminanti e sono deducibili in automatico come i parametri comportamentali. Per meglio comprendere questi aspetti, si riportano le tabelle di definizione prese in accordo alle ASCE 41:2010.
Figura 15: parametri di comportamento e di verifica delle cerniere plastiche di travi in c.a.
Figura 16: parametri di comportamento e di verifica di colonne in c.a.
SAP2000 ed ETABS integrano la procedura di taratura automatica delle cerniere plastiche basata su queste tabelle. A titolo di esempio si veda la Figura 15 in riferimento alla Figura 11. In una trave in c.a., la duttilità della stessa, rappresentabile dalla rotazione espressa con a dipende dai tre discriminanti descritti, in particolare viene seguita questa procedura:
- il programma controlla l’armatura superiore ed inferiore presente nel frame. Questa può essere passata direttamente: Figura 11, oppure dedotta da una progettazione automatica. Dall’armatura determina r, rapporto di armatura tesa e r’, rapporto di armatura compressa. Verranno calcolate due condizioni: per momenti negativi (fibra tesa superiore), momenti positivi (fibra tesa inferiore).
- Il programma chiede se il passo delle staffe è conforme (inferiore a d/3, con d altezza utile della sezione), oppure, non conforme (superiore a d/3).
- Il programma chiede da quale analisi prelevare il taglio, V, con il quale calcolare il terzo discriminante.
- Raccolti i primi tre discriminanti entra in tabella, interpolando gli stessi ed ottenendo la definizione di: a, b e c, come parametri di progetto della cerniera che insieme al momento resistente positivo e negativo, calcolato in automatico (di nuovo funzione dell’armatura, della sezione e dei materiali) rappresentano la definizione della legge comportamentale. Oltre a questi tre parametri, vengono dedotte le capacità rotazionali, in funzione del fatto che l’elemento sia primario o secondario; capacità rotazionali corrispondenti ai tre stati limite considerati: danno limitato, danno severo e prevenzione di collasso.
Un procedimento del tutto analogo viene seguito per le colonne. Per i setti si procederà ad una trattazione a fibre.
Cerniere plastiche del tipo a fibra
Le cerniere plastiche a fibre sono cerniere plastiche di interazione PMM, ovvero, lavorano contemporaneamente in interazione tra sforzo normale e momenti flettenti, sia essi semplici o deviati.
Si basano su l’assunzione che la legge momento-rotazione possa essere determinata trattando la sezione come un aggregato di fibre. In riferimento alla Figura 17, una qualsiasi sezione in c.a., viene scomposta automaticamente in un aggregato di fibre di cls, ognuna delle quali avente area pari alla sua porzione spettante, posizione del suo baricentro e con legge costitutiva del calcestruzzo non confinato o confinato utilizzando la comune definizione e parametrizzazione del modello di Mander, che tiene conto dell’armatura e del confinamento indotto da essa, e da una fibra per ogni armatura, avente area pari all’armatura stessa e legge costitutiva del materiale utilizzato per le armature.
Figura 17: composizione di una cerniera a fibre
Con questa schematizzazione è possibile parametrizzare qualsiasi sezione in automatico, senza limite di forma od armatura. La backbone è direttamente il momento-rotazione di questo aggregato di fibre ed i limiti di rotazione, utilizzati come capacità rotazionali della cerniera, sono deducibili dallo stato di danneggiamento delle singole fibre.
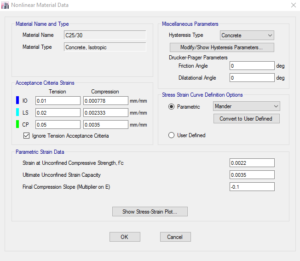
La procedura consigliata in questo caso è la seguente. Si parte definendo la legge costitutiva del materiale cls base, ovvero escluso la correzione che tiene conto, secondo il modello di Mander del confinamento.
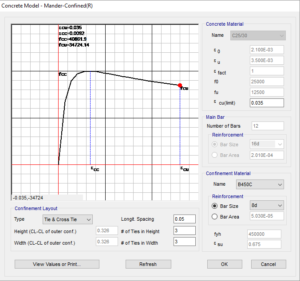
Figura 18: parametrizzazione del materiale secondo il modello di Mander
Si ipotizza un materiale di classe C25/30, avente i seguenti valori:
fck = 25 MPa; fcm = 25+8=33 MPa; ec1 = 2.2E-03; ecu = 3.5 E-03
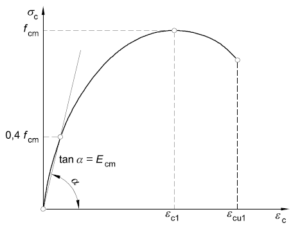
si veda la Figura 19 con la legge costitutiva adottata.
Figura 19: legge costitutiva del materiale base automaticamente definita
Definito il materiale base è possibile definire la sezione in Section Designer definendo i parametri necessari alla determinazione del confinamento.
Figura 20: assegnazione delle staffe per il confinamento e calcolo automatico della curva s-e del materiale confinato
Passate le informazioni delle staffe: passo, numero di bracci, diametro e materiale, viene automaticamente calcolata la nuova curva del materiale confinato e viene attribuito alla sezione.
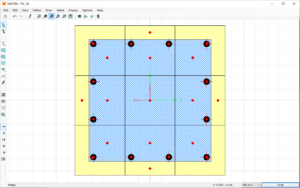
Le fibre vengono a questo punto ritracciate sulla base del doppio materiale.
Figura 21: tracciamento automatico delle fibre
Cerniere plastiche a fibre per i setti
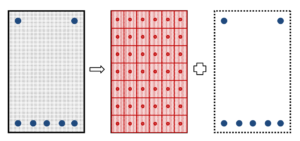
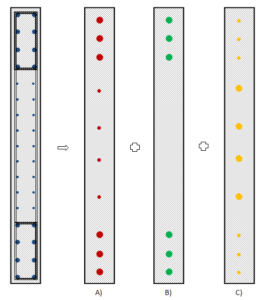
In ETABS2016 la trattazione di pareti non lineari viene gestita mediante una modellazione a fibre rappresentata in Figura 22. La parete, composta da porzione in cls confinata all’estremità della stessa, di una porzione di cls non confinato e delle armature viene schematizzata in automatico dal programma, passando le armature inserite nella parete, utilizzando tre strati di fibre.
Il primo strato, indicato con A nella figura, rappresenta le fibre delle armature inserite nella parete. Le armature vengono accorpate e poi suddivise in un certo numero di fibre. L’area corrispondente alle singole fibre, è la somma delle armature efferenti ad essa, la legge costitutiva è quella del materiale utilizzato. Il secondo strato, la lettera B, rappresenta il cls confinato. Presente solo nel caso di zona confinata all’estremità della parete, normalmente esteso il 20% della lunghezza della parete, ma comunque dato che viene richiesto nella definizione e quindi modificabile, anche in questo caso l’area delle singole fibre di cls, rappresenta l’area efferente di cls. L’ultimo strato, la lettera C, rappresenta il cls non confinato: quello fuori dalle staffe nella zona di estremità e la restante parte di cls all’interno della parete. Tutte le informazioni geometriche e di armatura necessarie sono passate mediante una finestra parametrica, le fibre vengono poi tracciate in automatico e possono essere visualizzate.
Figura 22: modellazione a fibre di una parete, procedura automatica in ETABS2016
In SAP2000 è possibile procedere analogamente, ma utilizzando l’elemento Shell di tipo Layered/NonLinear, sempre definito in via parametrica e quindi semplice da trattare.
Controllo di forza / controllo di spostamento
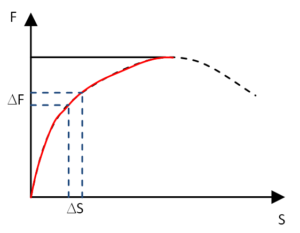
Un’analisi non lineare può essere effettuata a controllo di forza od a controllo di spostamento. Ognuna di queste analisi è un’analisi al passo. Per spiegare la differenza tra i due metodi, si faccia riferimento ad una qualsiasi risposta riportabile come grafico Forza-Spostamento, come qualitativamente rappresentata in Figura 23. Si immagini di utilizzare il metodo dell’analisi a controllo di forza. La forza complessiva da applicare, Ftot viene inizialmente divisa in porzioni costanti, degli incrementi di forza denominati DF. Ogni porzione, corrisponde alla Forza complessiva divisa il numero di passi che si vuole seguire. Ogni passo di analisi verrà applicato un incremento di forza DF, rispetto alla forza applicata al passo precedente. Ad ogni passo si avrà un incremento di spostamento DS, dipendente dalla rigidezza della struttura a quel passo. I DS non saranno generalmente costanti, a meno di strutture elastiche lineari. Questa analisi può percorrere la curva, fino alla sua sommità, intesa come forza massima. Arrivato a quel passo di analisi, nessun incremento possibile di forza potrà essere compatibile con la struttura, ed analiticamente si ha la perdita di convergenza numerica. In altre parole, un’analisi a controllo di forza non prevede una riduzione delle forze complessive, quindi può riprodurre solo un comportamento strettamente monotono crescente. Nella figura indicata, si potrà seguire solo il tratto evidenziato in rosso. Un’analisi a controllo di spostamento, invece, si applicano dei DF che possono essere sia positivi che negativi, imponendo però di avere un incremento di spostamento. Un comune errore è quello di pensare che in un’analisi del genere siano applicati degli spostamenti. Non è un’analisi a spostamento impresso, ma un’analisi in cui un sistema di forze viene fatto variare incrementando o diminuendo la magnitudo della forza del passo precedente. Condizione necessaria per la convergenza è invece che lo spostamento del punto controllato proceda in modo incrementale rispetto al passo precedente. Quindi, per avere convergenza, è necessario sempre scegliere un buon punto di controllo, che raggiunto livelli di forza per i quali sta avvenendo un evento (plasticizzazione, raggiungimento di carichi critici, rotture locali, meccanismi globali) proceda monotonamente, incrementando lo spostamento nella direzione e nel verso dei passi precedenti. In questo tipo di analisi, si possono percorrere rami discendenti, quindi in riferimento alla figura, sarà percorsa anche la parte tratteggiata. Un’analisi pushover, prevedendo la possibilità di avere delle rotture locali, o meccanismi che portano ad una riduzione di forza complessiva, deve essere fatta necessariamente a controllo di spostamento. Mentre l’analisi a controllo di forza, applica una forza nota in modulo, oltre che in distribuzione, un’analisi a controllo di spostamento, invece, applica una forza nota solo in distribuzione, ma non ancora in modulo. Quindi, per l’analisi gravitativa, condizione di partenza di un’analisi pushover, passo 1 della Figura 2, sarà svolta a controllo di forza, mentre le altre orizzontali saranno tutte a controllo di spostamento e partiranno dalla fine dell’analisi verticale.
Figura 23: controllo di forza vs controllo di spostamento
| Indietro | Prosegui |
|---|