Analisi della risposta dinamica di una fondazione di macchine vibranti – Steady State

Argomento: Valutazione della risposta dinamica di fondazioni a supporto di macchine vibranti. Analisi nel dominio delle frequenze. Steady State. Frequency dependent link. Smorzamento isteretico vs smorzamento viscoso lineare
Autore: Simone Caffè, simone.caffe@gmail.com
Contatto supporto CSi Italia: supporto@csi-italia.eu

Introduzione

Le fondazioni di macchine (e.g. turbine, compressori, alternatori ecc…), siano esse realizzate a mezzo di platee in calcestruzzo di grande spessore (palificate o meno), con telai a cavalletto (tipici delle turbine a vapore) o infine con deck in acciaio, forniscono una solida piattaforma sulla quale il macchinario, solitamente di considerevole peso, possa essere sostenuto e manutenuto.

Una vibrazione inaspettata può essere dannosa tanto per la macchina quanto per le componenti impiantistiche a servizio di questa, oltre a costituire una fonte di rischio per il personale addetto al funzionamento ed al controllo.

Qualora le vibrazioni diventino eccessive e incontrollabili, una macchina può arrestarsi improvvisamente provocando eventi anche catastrofici, quali la perdita improvvisa di una paletta del rotore (blade loss) o il corto circuito nel caso di un alternatore.

Il modo più conveniente per evitare questo tipo di eventi è quello di progettare la fondazione in modo che le ampiezze di vibrazione indotte dal macchinario risultino contenute entro i limiti di accettabilità richiesti dal Produttore (o dalle Specifiche Tecniche), scongiurando altresì fenomeni di risonanza.

Esistono da sempre approcci progettuali basati su regole empiriche atti a dimensionare le fondazioni in modo che possano essere sufficientemente rigide e massive da evitare idealmente gli effetti risonanti; è altresì vero che la complessità sempre maggiore dei suddetti macchinari unita alla ricerca di performance sempre più elevate e a basso impatto ambientale, indirizzano tanto l’analisi vibrazionale, quanto quella meccanica, verso l’utilizzo di strumenti sempre più evoluti atti a prevedere, nel modo più rigoroso possibile, la risposta del sistema fondazione più macchinario.

Partendo da questo presupposto è facile comprendere come le regole empiriche e la semplice analisi modale (NATURAL FREQUENCY ANALYSIS) costituiscano la base dalla quale partire per un corretto design di una fondazione di macchine, ma non possano altresì essere considerate l’unico strumento per effettuare una progettazione secondo lo stato dell’arte. Giocoforza sarà sempre necessario condurre analisi dinamiche nel dominio del tempo (TIME HISTORY) o della frequenza (STEADY STATE) atte a valutare l’effettivo valore delle ampiezze di vibrazione da confrontarsi con i limiti di accettabilità delle stesse.

Per studiare correttamente l’interazione suolo + struttura + macchinario, è solitamente consigliato il metodo della “funzione di impedenza” all’interno di un’analisi Steady State tenendo presente che la rigidezza dinamica del terreno e i coefficienti di smorzamento dipendono dalla frequenza, e che pertanto sarà necessario considerare questa variabilità in sede di analisi (ad esempio con l’utilizzo dei cosiddetti FDL, Frequency Dependent Link).

Nel seguito si andranno sinteticamente a descrivere, i tre approcci comunemente utilizzati per il dimensionamento e la progettazione delle fondazioni di macchine.

Metodo empirico

Il suddetto metodo può essere utilizzato nel caso di macchinari (es. generatori o piccole stazioni di pompaggio) in cui le forze di squilibrio indotte dalla macchina risultino pressocché insignificanti. In tale caso, al fine limitarne le vibrazioni, sarà sufficiente assicurarsi che la massa della fondazione sia almeno tre volte superiore a quella della macchina nel caso di macchina rotante o almeno cinque volte superiore nel caso di una macchina alternativa (le masse delle macchine sono da intendersi come somma delle parti fisse e di quelle mobili).

Metodo delle frequenze naturali

Nel caso in cui si vogliano escludere effetti di risonanza del sistema durante la fase operativa di funzionamento del macchinario, si rende necessario effettuare l’analisi modale. La ricerca delle frequenze proprie di vibrazione del sistema fondazione + struttura + macchinario, può essere utilizzata per dimostrare una sufficiente separazione tra le frequenze naturali del suddetto sistema e la frequenza di lavoro del macchinario. Una sufficiente separazione delle frequenze si ottiene quando qualsiasi risonanza naturale primaria del sistema risulta o minore di 0.50 o superiore a 1.50 volte la frequenza di eccitazione.  Spesso il suddetto requisito è difficile da ottenersi con riferimento a tutte le frequenze primarie, in tale caso si rende necessaria l’analisi dinamica.

Analisi forzata smorzata

Nel caso in cui si abbia a che fare con macchinari particolarmente sensibili alle vibrazioni, o altresì nel caso in cui i requisiti legati alla separazione modale non siano soddisfatti, si rende necessaria l’analisi della risposta alle vibrazioni forzate utilizzando o un’analisi dinamica nel dominio del tempo o un’analisi dinamica nel dominio della frequenza. Rispetto all’analisi modale, la cui risposta è correlata unicamente alla massa M ed alla rigidezza elastica K_st del sistema, nel caso dell’analisi armonica, un ruolo fondamentale è rivestito dallo smorzamento C (sia dallo smorzamento modale sia dallo smorzamento del terreno o dei pali di fondazione).

Nell’analisi forzata smorzata, si considera un sistema dinamico che viene sottoposto a una forza esterna periodica o transitoria, che nel caso di fondazioni di macchine è rappresentata dalla forza centrifuga dovuta allo sbilanciamento del rotore, funzione del cosiddetto AOU (amount of unbalance) e del quadrato della velocità angolare dello stesso. Lo smorzamento può essere descritto come quel fattore che influenza il modo in cui il sistema risponde ad una determinata forza nel tempo.

Per eseguire un’analisi forzata smorzata, è necessario conoscere le caratteristiche del sistema, come la sua massa M, la rigidezza elastica K_st, lo smorzamento C e la forza esterna applicata. Queste informazioni possono essere utilizzate per formulare l’equazione del moto del sistema.

Dove: M è la massa del sistema, C è il coefficiente di smorzamento, K_st è la costante di rigidezza, u è lo spostamento del sistema rispetto alla sua posizione di equilibrio, u’ è la velocità, u’’ è l’accelerazione e P(t) è la forza armonica esterna applicata al sistema, in funzione del tempo t.

La forza eccitante P(t) può essere riscritta nel dominio della frequenza nel modo seguente:

Analogamente possono essere riscritti termini che rappresentano lo spostamento u, la velocità u’ e l’accelerazione u’’:

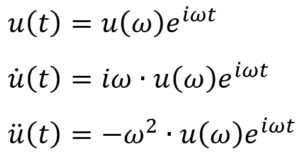
Sostituendo i suddetti termini nell’equazione del moto scritta nel dominio del tempo, si perviene ad una formulazione alternativa della medesima equazione scritta nel dominio della frequenza:

Dove il termine entro parentesi quadre rappresenta la matrice dinamica:

E la soluzione dell’equazione, ovvero la risposta del sistema all’eccitazione dovuta alla forzante armonica è pari a:

Caso studio

Il caso studio si pone come obiettivo quello di mettere a confronto i risultati di un’analisi armonica condotta con software commerciali tipo MathCAD o shareware tipo SMath Studio, con quelli ottenuti mediante analisi Steady State effettuate con il Codice di Calcolo agli Elementi Finiti SAP2000.

A partire dalla definizione della geometria e delle proprietà meccaniche degli elementi costituenti il cavalletto di supporto di un motore elettrico, verranno costruite passo passo le matrici di rigidezza elastica, di massa e di smorzamento del sistema pali + fondazione + struttura + macchinario. Verranno altresì definite le proprietà dinamiche del sistema oltre ai carichi di sbilanciamento che il motore esercita sul sistema durante le fasi operative di lavoro, e attraverso semplici operazioni matriciali verranno determinate le funzioni di risposta in termini di spostamento e velocità di vibrazione.

Il modello di calcolo verrà costruito simultaneamente alla definizione delle operazioni matriciali eseguite con MathCAD in modo da rendere esplicita all’utente la procedura numerica e analitica con la quale andare ad effettuare un’analisi di risposta in frequenza.

Guida passo-passo, scarica modelli.