Il tuo carrello è attualmente vuoto!
Modellazione ed analisi di strutture protette sismicamente con controventi dissipativi
Lo scopo di questo documento è quello di descrivere le procedure FEM e numeriche per studiare interventi di adeguamento o miglioramento sismico condotti mediante dissipazione supplementare di energia. Verranno descritte le procedure atte alla riproduzione numerica di cicli isteretici e di risposta di detti dispositivi e le procedure di analisi che condurranno da una parte al dimensionamento degli stessi e dall’altra alla verifica strutturale della struttura che li ospita. Di seguito si definirà struttura nuda, il modello numerico che descrive il comportamento statico e dinamico della struttura che ospita i dispositivi e di struttura protetta, riferendosi alla stessa struttura nella quale si opera l’installazione di dispositivi di dissipazione, principalmente allo scopo di migliorare il comportamento sismico generale. L’inserimento di controventi dissipativi, che ospitano tale dispositivi, ha lo scopo principale di proteggere una struttura esistente, quindi nel presente documento si fa l’ipotesi che si voglia effettuare un intervento di miglioramento/adeguamento. L’ipotesi di base sarà che la protezione raggiunta con tale metodologia è talmente elevata da consentire di immaginare la dissipazione concentrata solo nei dispositivi e non nella struttura stessa. In altre parole, si immagina la struttura nuda rimanere in campo elastico, a seguito dell’incremento di performance raggiunto dall’intervento, minimizzando il danno su di essa, o comunque non ricorrendo ad esso per l’abbattimento delle forze sismiche. E’ oramai noto, che in una progettazione tradizionale, per contro di quella in esame, si ricorre al dimensionamento corretto degli elementi strutturali, che mediante il rispetto delle prescrizioni sismiche e metodi di gerarchia delle resistenze, hanno una sovra resistenza ed una duttilità tale da poter incassare un certo livello di danno. Danno, grazie al quale si ha una dissipazione energetica, che normalmente viene messa in conto come sconto delle azioni sismiche per effetto di un fattore di struttura, da scegliere in modo aprioristico, in fase di progettazione o da valutare sulla base del dettaglio strutturale esistente per una struttura già realizzata. In una struttura protetta, la dissipazione è ad opera di comportamenti non lineari insiti nei dispositivi, per lo più distribuiti all’interno della compagine strutturale. Quando la struttura, che ospita tali sistemi, è multipiano, ovvero, i dispositivi sono disposti su più livelli che inbteragiscono dinamicamente tra di loro, è impensabile poter approcciare con modellazioni lineari e poter tenere in conto del beneficio indotto dai dispositivi. Quindi, sarà necessario, ma vedremo anche più logico ricorrere a metodologie di analisi non lineari.
Quadro normativo di riferimento
Pur mantenendo un approccio trasversale valido per tutte le normative, in questo documento si adotteranno procedure scelte in accordo alle seguenti normative tecniche:
- M. 14/01/2008 – Nuove Norme Tecniche per le Costruzioni (v. § 8)
- Circolare 02/02/2009 n°617/C.S.LL.PP. – Circolare applicativa (v. § C8 e § C8A)
Normative internazionali di rilievo:
- EN 1998-3:2005 – Eurocode 8 – Design of structures for earthquake resistance – Part 3: Assessment and retrofitting of buildings
- FEMA 356 – Prestandard and Commentary for the Seismic Rehabilitation of Buildings
Leggi costitutive non lineari
Nel codice di calcolo SAP2000 (CSi – Computers and Structures inc.) le proprietà inelastiche vengono inserite mediante elementi non lineari a uno o a due nodi chiamati NLLINK (Non Linear Link). Gli NLLINK possono essere definiti indipendentemente nei sei gradi di libertà. Gli NLLINK sono così suddivisi:
- Linear
- Viscous Damper: smorzamento viscoso secondo la legge di Maxwell
- Friction Spring Damper: smorzamento isteretico su base attritiva
- Gap: apertura/giunto resistente a sola compressione
- Hook: gancio con apertura resistente a sola trazione
- Multilineare elastico: legge multi-lineare elastica monoassiale
- Multilineare plastico: legge elastoplastica monoassiale (modello secondo Wen oppure ad incrudimento cinematico, Pivot o Takeda)
- Isolatore ad attrito (Friction-pendulum base isolator) che può essere usato come un appoggio mono-direzionale ad attrito
- Isolatore plastico bi-assiale (esempio di isolatore in gomma).
Di seguito verranno illustrate le modellazioni degli elementi base. I dispositivi in commercio associano più comportamenti, per esempio uniscono le proprietà isteretiche dell’acciaio a quelle di un fluido viscoso, combinandole in serie o in parallelo per dotare i dispositivi delle caratteristiche di modesta resistenza a basse velocità (evitando così coazioni termiche) e di alta dissipazione durante gli shock sismici. Per riprodurre informa numerica questi comportamenti sarà quindi sufficiente unire diversi elementi base.
Proprietà di un elemento linear
Molla elastica lineare con gradi di libertà linearmente indipendenti od accoppiati sui 6 DOF.
Proprietà di un elemento viscous damper
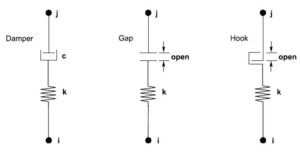
Il modello di smorzamento viscoso è basato sul modello viscoelastico di Maxwell (Malvern, 1969) è costituito da uno smorzatore a viscosità non lineare in serie con una molla. Si veda la Figura 1.
Figura 1: Damper, Gap, Hook
La legge non lineare di forza-deformazione è dato da:
[1]
dove k è la costante elastica della molla, la c è il coefficiente di smorzamento, cexp è l’esponente della velocità, il è la deformazione subita dalla molla elastica e la è la velocità di deformazione.
La gamma pratica del coefficiente cexp è compresa fra 0.15 e 2.0, anche se difficilmente si supera 0.3. La deformazione totale dell’elemento risulterà pertanto somma della deformazione della componente elastica e di quella viscosa.
[2]
Per uno smorzatore puro l’effetto della molla può essere reso trascurabile rendendolo sufficiente rigido.
La rigidezza della componente elastica deve essere grande abbastanza da far risultare il periodo caratteristico del sistema molla-smorzatore dato da
(quando l’esponente è 1) un ordine di grandezza minore della grandezza dei passi di carico. Il passo di carico rappresenta l’intervallo di tempo nel quale il valore del carico cambia. Fisicamente tale rigidezza rappresenta la pendenza di scarico del ciclo ed è dovuta alla comprimibilità del fluido contenuto internamente al ciclindro.
Proprietà di elementi Gap e Hook
Elementi elastici non lineari dotati di una apertura posta in serie ad una molla. L’elemento Gap è dotato di sola resistenza a compressione, può essere utilizzato per simulare dei battimenti strutturali, per esempio dovuti alla chiusura di un giunto, oppure, nello specifico per simulare il fondo corsa di un dispositivo. L’elemento Hook è il suo duale, ovvero, capace i resistere solo a trazione. Si veda la Figura 1.
Proprietà di un elemento multilineare elastico
La relazione Forza-Deformazione è data da una curva n-lineare elastica. La curva n-lineare rappresenta rigidezze costanti a tratti.
Il comportamento è non lineare ma elastico. Questo vuol dire che il l’elemento multilineare è un elemento elastico la cui curva è n-lineare e la stessa curva viene seguita in fase di carico e in fase di scarico senza avere isteresi.
Proprietà di un elemento multilineare plastico
La relazione Forza-Deformazione è data da una curva n-lineare elastica. La curva n-lineare rappresenta rigidezze costanti a tratti. La curva in fase di scarico deriva da quelle di carico secondo tre diversi modelli isteretici: Takeda, Pivot o ad incrudimento cinematico.
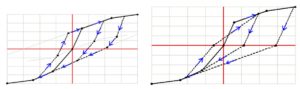
Nelle figure seguenti sono riportati i diversi percorsi di scarico seguiti.
Figura 2: a) incrudimento cinematico, b) ciclo Takeda
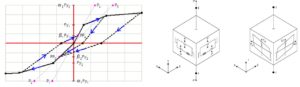
Figura 3: a) ciclo Pivot, b) schema di un dispositivo di link di tipo Friction Pendulum Isolator, c) schema link Rubber Isolator
Proprietà di un isolatore ad attrito – Friction Pendulum isolator
Questo è un isolatore biassiale ad attrito che accoppia le proprietà di attrito per le due deformazioni a taglio. Le deformazioni a taglio avvengono con le ipotesi di slittamento su una superficie. Questo elemento accoppia anche funzione di Gap assiale (ovvero è incapace di resistere a trazione) ed è resistente a momento nelle 2 direzioni. In pratica si usa per modellare il comportamento dei classici dispositivi di appoggio (dispositivi a piatti in acciaio lucidati o trattati con teflon).
Il modello di attrito è basato sul comportamento isteretico proposto da Wen (1976), e Park, Wen ed Ang (1986) e suggerito per analisi in occasione di isolamento alla base Nagarajaiah, Reinhorn e Constantinou (1991). Il comportamento del pendolo è come quello proposto da Zayas e da Low (1990).
Un valore pari a zero del raggio indica una superficie di scorrimento piatta e la corrispondente azione di taglio risulta nulla.
Se la superficie di slittamento è concava, il dispositivo oltre a garantire uno slittamento e un comportamento isteretico prodotto dall’attrito ha la duplice funzione di ricentraggio, ovvero, la capacità di tornare nella posizione iniziale successivamente all’azione sismica.
Proprietà di un isolatore plastico biassiale
Questo è un isolatore isteretico biassiale che accoppia le proprietà di plasticità deformazioni a taglio e le proprietà lineari di rigidezza efficace per le quattro deformazioni restanti. Il modello di plasticità è basato sul comportamento isteretico proposto da Wen (1976) e Park, Wen ed Ang (1986) e suggerito per l’isolamento alla base trattato da Nagarajaiah, da Reinhorn e da Constantinou (1991). Si veda la Figura 3c.
Questo elemento viene utilizzato per riprodurre il comportamento di dispositivi di isolamento commerciali noti come HDRB (High Damping Rubber Isolator), dove le proprietà isteretiche sono affidate ad una matrice elastomerici che contiene delle piastre di acciaio con funzione di armatura.
Proprietà di un Friction Spring Damper
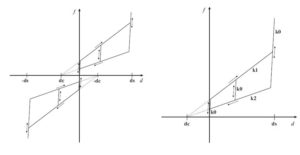
Link caratterizzato da rigidezze governabili per la fase di carico e scarico, da un limite deformativo e dalla presenza di un precarico. Basato sul ciclo isteretico del dispositivo presentato da: Filiatrault, A., Tremblay, R., Kar,R.(2000). Performance Evaluation of Friction Spring Seismic Damper, Journal of Structural Engineering, Aprile 2000, n°491.
Figura 4: ciclo isteretico di un Friction Spring Damper
Tecniche di analisi dinamica non lineare
Integrazione diretta
L’approccio più generale per determinare la risposta dinamica di una struttura consiste nella integrazione diretta delle equazioni di equilibrio, ossia, nel soddisfare le equazioni di moto in un numero discreto di intervalli di tempo , tramite un apposito algoritmo, di tipo esplicito od implicito. Nel primo caso, come noto, la soluzione al passo t viene ricavata in base ai valori individuati al precedente passo, . Per i metodi impliciti, invece, la soluzione dipende anche dai valori delle grandezze di risposta al passo t. I metodi espliciti sono condizionatamente stabili rispetto a , mentre gli impliciti sono per lo più incondizionatamente stabili.
Tra i diversi algoritmi proposti in letteratura (Newmark, Wilson-q, Hilbert ecc), il più ampiamente utilizzato è quello di Newmark. In tale metodo, l’equazione di moto al generico passo t può essere espressa come:
[3]
Lo spostamento e la velocità possono essere scritte ricorrendo ad uno sviluppo in serie di Taylor contenente n termini:
[4]
Troncando le espressioni [4] al terzo termine dello sviluppo, ossia alla derivata terza, e trasformando i termini e
in coefficienti arbitrari, rispettivamente denominati e , che tengono conto dell’approssimazione legata al troncamento, si ottiene:
[5]
Ponendo, quindi, l’ipotesi di accelerazione variabile linearmente all’interno del passo di tempo, la derivata terza dello spostamento può essere scritta:
[6]
Sostituendo la [6] nelle equazioni [5] si ricavano infine, le seguenti espressioni:
[7]
che costituiscono la formulazione generale dell’algoritmo di Newmark, le cui proprietà numeriche sono determinate dalla scelta dei coefficienti e . Il metodo prevede di risolvere le equazioni [3] e[7] iterativamente per ogni passo di tempo e per ogni grado di libertà della struttura. I termini delle accelerazioni sono calcolati dalla [3], dividendo per le masse associate ai diversi gradi di libertà.
La condizione di stabilità per il metodo di Newmark può essere scritta come:
[8]
in cui wmax, Tmin rappresentano la massima pulsazione propria ed il minimo periodo proprio significativi nella risposta modale del modello strutturale. Ponendo =0 e =1/2 nelle [7], si ottiene la versione esplicita dell’algoritmo di Newmark. La condizione =1/4 e =1/2 definisce, altresì, il metodo dell’accelerazione media costante, implicito ed incondizionatamente stabile per analisi lineari, nonché numericamente non dissipativo.
Tra i restanti principali algoritmi d’integrazione presenti in letteratura, piuttosto diffusamente utilizzato è anche quello che va sotto il nome di Wilson- , che rappresenta una variante del metodo generale di Newmark, ottenuta mediante l’introduzione di un parametro q, secondo quanto di seguito espresso:
[9]
Si ottiene, in questo caso, una variazione lineare dell’accelerazione nell’intervallo temporale esteso . L’algoritmo risulta incondizionatamente stabile in problemi lineari per >1.37, e la formulazione più classica è quella in cui viene assunto =1.4.
FNA – Fast non linear analysis
Le strutture presentano generalmente un limitato numero di membrature impegnate in campo non lineare durante un’azione sismica; tale numero scende sensibilmente per quelle dotate di elementi di dissipazione supplementare di energia o di dispositivi di isolamento sismico, mantenendosi essenzialmente in campo elastico la risposta della restante parte dell’organismo strutturale. Nel modello computazionale, soprattutto nell’ambito di problemi dinamici, risulta quindi opportuno evitare un approccio di analisi non lineare a “forza bruta”, ossia, mediante integrazione diretta al passo delle equazioni di moto, il cui processo risolutivo preveda l’aggiornamento della matrice di rigidezza ad ogni passo di integrazione.
L’alternativa, valida per modelli a non linearità concentrate, è stata formulata da Wilson (2002) e va sotto il nome di “Fast Nonlinear Analysis” (FNA). Tale strategia, nata dalla estensione al campo non lineare del metodo di sovrapposizione modale, si basa sul disaccoppiamento delle equazioni di moto. Questo approccio prevede di separare i gradi di libertà a comportamento lineare da quelli a comportamento non lineare, definendo un sistema di equazioni di moto su base di autovettori determinati con il metodo di Ritz (mediante l’uso di “forme” dipendenti dal carico). Conseguentemente, ad ogni passo di integrazione, soltanto la risposta degli elementi non lineari viene sottoposta ad una procedura incrementale-iterativa, mentre le matrici di rigidezza e di smorzamento viscoso lineare relative alla più ampia parte della struttura, caratterizzata da una risposta di tipo elastico, rimangono quelle di primo assemblaggio, così come valutate al passo iniziale. Di norma, queste matrici vengono calcolate nella condizione indeformata, anche se possono essere ottenute come ultimo passo di una precedente analisi statica non lineare e contenere, pertanto, uno stato deformativo e tensionale imposto da una condizione variata di partenza.
Il metodo si basa sul presupposto di separare il vettore complessivo delle forze interne ed esterne non lineari Rnl(t) (dovute a comportamento non lineare concentrato in un numero limitato di elementi), dal vettore delle forze interne ed esterne elastiche e viscose lineari della restante parte della struttura. Pertanto, al generico istante t si può scrivere:
[10]
dove Kl è la matrice di rigidezza degli elementi lineari (tutti gli elementi, esclusi gli “NLLINK”); C la matrice di smorzamento; M la matrice delle masse; Rnl (t) il vettore delle forze dei gradi di libertà degli elementi non lineari; sono i vettori di spostamento, velocità ed accelerazione relativa rispetto al suolo; R(t) è il vettore delle forze applicate. Le matrici M, C, Kl sono di ordine NxN, ossia, scritte per tutti i gradi di libertà del modello. Gli elementi non lineari, infatti, sono comunque dotati di componenti lineari (di rigidezza eventualmente nulla) per ogni grado di libertà non lineare attivato.
Raccogliendo nella matrice Kenl le rigidezze elastiche degli elementi non lineari, è possibile scrivere la relazione [10] come:
[11]
dalla quale deriva:
[12]
in cui:
è la matrice di rigidezza elastica “globale” e rappresenta il vettore “efficace” dei carichi esterni, inclusivo degli effetti di risposta di tutti gli elementi non lineari. Questi ultimi, pertanto, attraverso il termine Rnl(t), restano confinati al solo secondo membro dell’equazione risolvente (da valutarsi mediante processo iterativo).
La risoluzione al passo della [12], come nel caso di analisi per sovrapposizione modale, viene preceduta dalla fase di determinazione degli autovettori che sono racchiusi nella matrice utilizzata come base per la scrittura e la scomposizione delle equazioni del moto. Tali vettori devono soddisfare le condizioni di ortogonalità:
[13]
dove I è la matrice di identità e la matrice diagonale contenente gli autovalori, entrambe di dimensioni NrxNr (essendo Nr il numero di forme modali prescelto per rappresentare il sistema). La risposta della struttura può quindi essere scritta in coordinate modali Y(t) come segue:
[14]
Sostituendo tali espressioni nella [12] e pre-moltiplicando i vari termini per , si ottiene:
[15]
in cui il termine delle forze modali è dato da:
[16]
Esprimendo le deformazioni degli elementi non lineari in funzione delle coordinate modali e della relativa matrice di trasformazione T, indipendente dal tempo, si ha:
[17]
[18]
dove fnl(t) è il vettore delle forze di reazione esercitate dagli elementi non lineari e Kl,enl è la matrice degli stessi elementi definita, termine per termine, nei rispettivi sistemi di riferimento locali. Quindi, attraverso le comuni tecniche applicate ai metodi basati sulla scomposizione modale, la [15] viene risolta aggiornando ad ogni passo solo il vettore contenente le forze non lineari, lasciando invariate le matrici di sistema.
Risulta immediatamente evidente il vantaggio computazionale di questo metodo rispetto ad algoritmi di integrazione diretta al passo. Nel caso di quantità percentualmente limitate di gradi di libertà non lineari, sul totale di quelli posseduti dal modello computazionale, questi ultimi richiedono, infatti, l’aggiornamento ad ogni passo dell’intera matrice di rigidezza, con sensibili incrementi dei tempi di elaborazione e delle risorse computazionali necessarie per la risoluzione del problema dinamico. Da un confronto dei tempi di calcolo necessari alla risoluzione, con analisi FNA o con l’integrazione diretta mediante il metodo esplicito di Newmark, di alcuni modelli assunti a titolo d’esempio, emergono riduzioni di un fattore pari ad almeno 100, nel primo caso, con pari accuratezza numerica.
Il metodo FNA può essere impiegato, per definizione, nei casi in cui la matrice di rigidezza si mantenga costante per tutta l’analisi, e pertanto, risulta inapplicabile ai problemi in cui non siano trascurabili gli effetti del secondo ordine sugli spostamenti. In tali casi, si rende necessario procedere all’integrazione diretta delle equazioni del moto.
Nota sul metodo di analisi modale secondo Ritz in alternativa al metodo classico agli autovalori
Nell’analisi di molte strutture, la risposta dinamica dei modi ad alta frequenza può essere significativa. Nell’uso del metodo classico degli autovettori, per analisi basate sulla sovrapposizione modale, come analisi spettrale o FNA, sono stati sviluppati metodi per migliorare la qualità dei risultati ottenuti e la predizione del comportamento dinamico della struttura: metodi basati sul “controllo della massa persa”, metodi di “correzione statica”.
La “correzione statica” consiste nello stimare la bontà del numero di modi considerato, rapportando (in termini energetici) la soluzione esatta (su tutti i gradi di libertà) di un modello soggetto ad un carico statico arbitrario, con la soluzione ottenuta con il sistema di gradi di libertà ridotto ai soli modi di vibrare. Nel caso in cui tale controllo lo richieda, la procedura di “correzione statica” modifica alcuni autovettori in modo da rendere accettabile tale rapporto energetico.
Nel metodo di Ritz viene applicata una correzione agli autovettori in modo da compensare gli errori indotti dal trascurare i modi superiori. In altre parole, immaginiamo un sistema costituito da N gradi di libertà. Si chiede di calcolare m modi di vibrare, con m<
Una analisi FNA, essendo basata sul disaccoppiamento su base modale, deve essere preceduta da un’analisi modale effettuata con il metodo di Ritz, scegliendo un numero di modi di vibrare sufficientemente alto. Una buona regola consiste nello scegliere un numero di modi tali da attivare tutta la massa della struttura, più un modo per ogni grado di libertà associato a NLLINK. Immaginando per esempio di attivare la quasi totalità della massa con 15 modi e di avere 100 link non lineari, ognuno con 3 dof attivi, il minimo numero di modi da considerare è 315. Oltre a questo accorgimento, si dovranno passare come vettori di carico di Ritz le seguenti opzioni:
Accelerazioni Uy, Uy ed Rz, anche la voce “Link All”. L’accelerazione Uz o vettori di carico verticali, saranno da includere nel caso si abbia link che si attivano per carichi gravitativi, per esempio link ad attrito. Si veda la Figura 5 per un esempio
Figura 5: definizione di analisi modale con il metodo di Ritz
Smorzamento viscoso lineare equivalente additivo alle analisi dinamiche non lineari, definizione secondo Rayleigh
Una struttura a comportamento elastico dissipa energia attraverso diversi meccanismi. Questo normalmente viene tenuto in conto mediante uno smorzamento viscoso, detto anche viscosità lineare equivalente.
Quando una struttura si snerva dissipa molta energia mediante meccanismi plastici. Questa dissipazione energetica è quantificabile come area sottesa in un ciclo isteretico ottenuto dalla legge Forza-Spostamento (Momento-Rotazione) di questi meccanismi plastici. Quello di cui ci occupiamo adesso non è la dissipazione energetica per effetto di danno, ma una dissipazione energetica propria di una struttura elastica. Anche in strutture in cui si ha un comportamento plastico (es. formazione di cerniere plastiche, o strutture protette mediante dispositivi di dissipazione) si ha comunque una dissipazione viscosa per la fase elastica.
In analisi spettrali si tiene in conto di questa dissipazione viscosa lineare utilizzando un rapporto di smorzamento critico del 5% e tracciando gli spettri di risposta utilizzando tale rapporto.
Vediamo come tenere in conto della componente dissipativa viscosa anche in analisi dinamiche non lineari (analisi al passo o Time History).
In una analisi al passo, in ogni istante di tempo deve essere soddisfatta la seguente relazione:
La matrice di rigidezza e di massa, K e M sono facilmente definibili, necessita una definizione anche la matrice di smorzamento C.
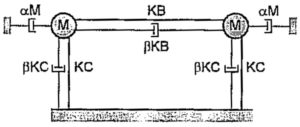
Secondo l’ipotesi di Rayleigh, una generica struttura può essere schematizzata come rappresentato in Figura 5.
Figura 6: schematizzazione alla Rayleigh di una struttura con i termini di smorzamento
Il termine M rappresenta uno smorzamento proporzionale alla massa è connesso a terra. Rappresenta una forza di smorzamento esterna.
Il termine K rappresenta uno smorzamento proporzionale alla rigidezza è parallelo agli elementi. Rappresenta una forza di smorzamento interna.
La matrice di smorzamento C è ottenuta da: C = M + K
Il significato fisico è chiaro, la scelta dei parametri e non è chiara ed univoca.
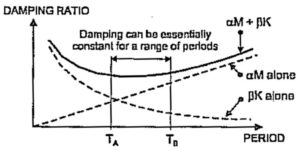
Il rapporto di smorzamento può essere diagrammato rispetto al periodo come riportato in
Figura 7: rapporto di smorzamento critico al variare del periodo, secondo la definizione di Rayleigh
In analisi lineari, i coefficienti e possono essere scelti in modo da rendere essenzialmente costante lo smorzamento all’interno di un range di periodo. Un possibile metodo è:
Scegliere TB = 0.9 T1, TA = 0.2 T1
Dove T1 è il primo modo della struttura.
Fissare ad un valore tipico (es ) il rapporto di smorzamento in corrispondenza dei due periodi.
Lo smorzamento è più alto nei modi ad alta frequenza, questo è generalmente buono per ridurre problemi numerici. Tuttavia, in analisi non lineare, per elementi che hanno una forte rigidezza iniziale (comportamento rigido-plastico) si rischia di introdurre uno smorzamento lineare equivalente troppo elevato e non realistico. Per ridurre questo problema, si consiglia di impostare i valori e a livello di materiale, in modo da escludere automaticamente i link, per i quali spesso si ha la necessità di fissare i primi rami di rigidezza elastica in modo arbitrariamente rigido, producendo, per effetto delle definizioni viste rapporti di smorzamento viscoso lineare equivalente altrettanto alti.
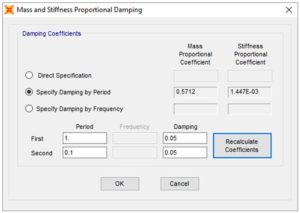
Nel caso di utilizzo di metodi di integrazione diretta, si è costretti ad utilizzare lo smorzamento viscoso lineare equivalente secondo questa procedura.
Figura 8: smorzamento viscoso lineare equivalente, definizione in analisi
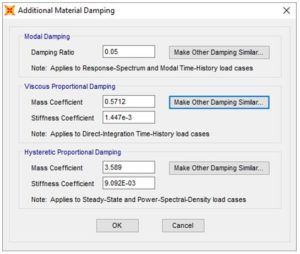
Figura 9: definizione dello smorzamento viscoso lineare equivalente nel materiale
In SAP2000, ETABS o CSiBridge, ci sono due metodi alternativi per passare lo smorzamento viscoso lineare equivalente valido per un’analisi dinamica non lineare definita con il metodo dell’integrazione diretta: nella definizione stessa dell’analisi (Figura 8) e nella definizione del materiale (Figura 9).
Normalmente, si suggerisce di passare e , i due fattori proporzionali alla massa ed alla rigidezza del sistema direttamente a livello di materiale, lasciando a zero quello dell’analisi, in questo modo si potranno escludere i termini proporzionali alla rigidezza derivanti da elementi link, spesso definiti con valori arbitrariamente alti della stessa.
Smorzamento viscoso lineare equivalente additivo alle analisi dinamiche non lineari, definizione modale
In analisi lineare od in analisi non lineare in cui sia applicabile un metodo di disaccoppiamento delle equazioni di moto su base modale, la struttura vibra in modo indipendente in ogni modo.
Figura 10: definizioni dello smorzamento viscoso lineare equivalente di tipo modale
Lo smorzamento modale coglie sia effetti interni che esterni, le forze non sono però uguali di quelle di Rayleigh. Lo smorzamento modale rimane costante durante l’analisi anche al variare della rigidezza della struttura. E’ molto semplice definire ed utilizzare questo metodo, altro vantaggio nell’utilizzo della analisi FNA.
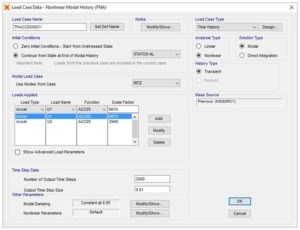
Figura 11: definizione di un’analisi FNA
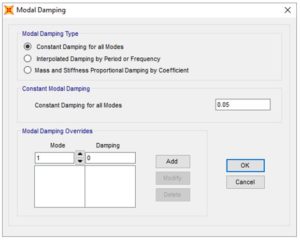
Figura 12: definizione dello smorzamento viscoso lineare equivalente in un’analisi FNA
Nella Figura 11 è visibile la definizione di un’analisi FNA, mentre in Figura 12 è possibile vedere come impostare lo smorzamento viscoso lineare equivalente di un’analisi FNA. Esso è operativamente più semplice, dal momento, che è sufficiente definire il rapporto di smorzamento che verrà computato per tutte le componenti soggette a deformazioni elastiche del modello.
| Indietro | Prosegui |
|---|